DEFCON quals | Rev ncHEVjuw.txt

Reverse Golly DEFCON
发布日期:   2024-09-15

DEFCON quals | Rev ncHEVjuw.txt

“电路是怎么构成CPU的？你可以这么想象，现在假想你已经控制了电路，可以任意的描述电路就可以把电路做出来，然后从这一步开始，你想要做一个CPU出来，忽略一些具体的细节，只关注最关键的部分，这 个过程能不能描述出来——这样吧，不如我直接给你个题，你可以判断下这块够不够了。”

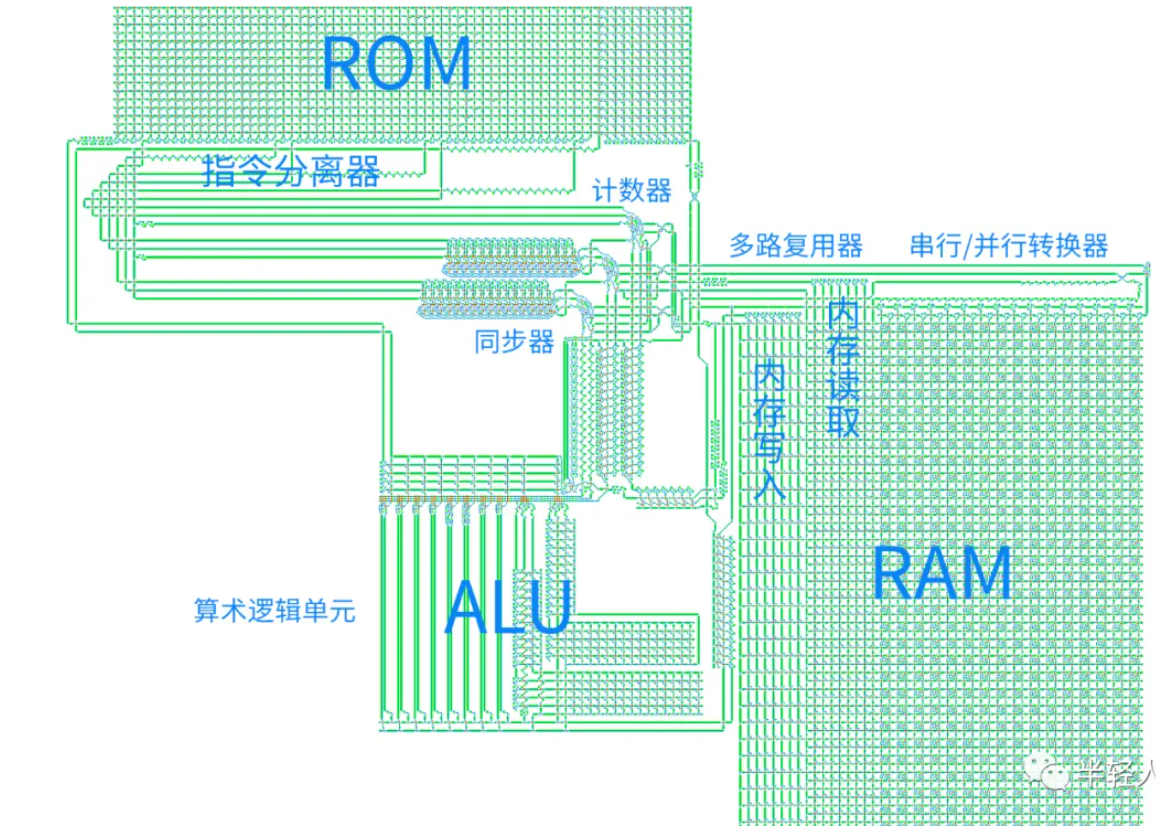
丁佬说用Golly打开，Golly存储格式为.rle，修改文件后缀，打开是一个CPU（小鳄鱼）

感觉思路大概是通过CPU的运行，通过程序的底层运行，还原程序，得到flag——

主要还是考CPU组成

尝试运行，一闪一闪的——

屏幕截图 2024-09-13 220336

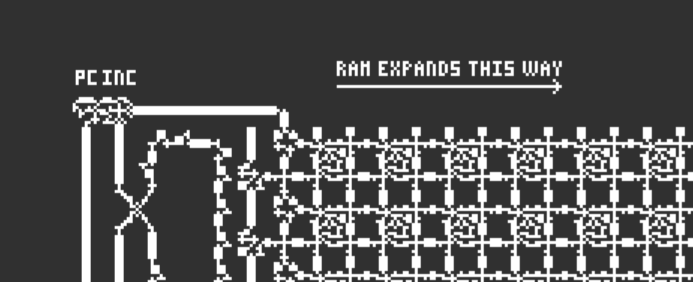
拉近再看，ROM，ROM EXPANDS THIS WAY<—

ROM（Read Only Memory）只读存储器

img

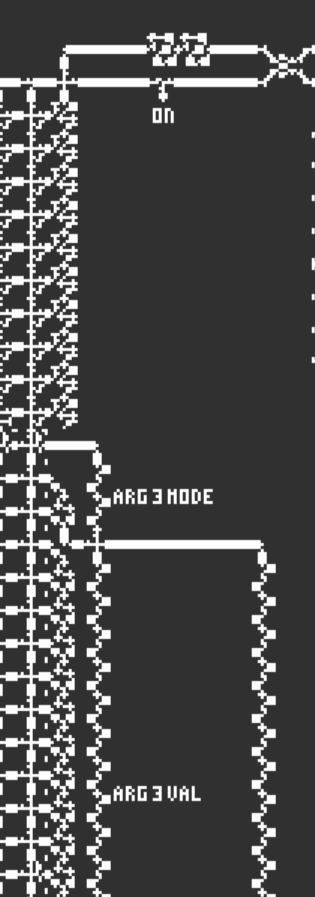
ON——开关

ARG i MODE 操作数的寻址方式

ARG i VAL 实际操作数的值

img

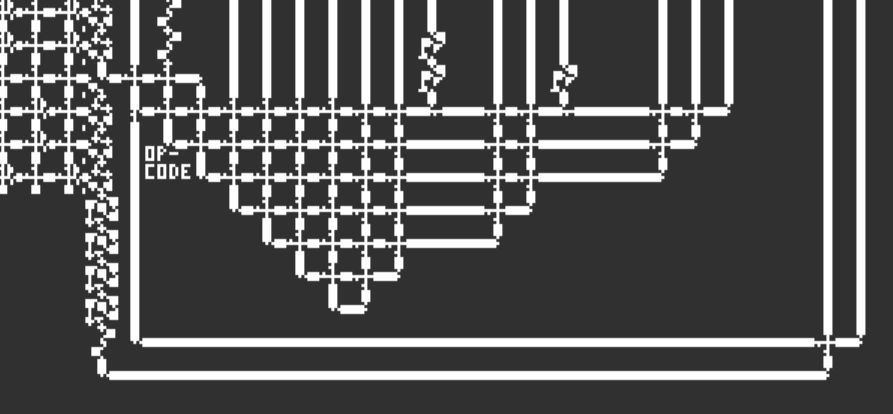
OpCode

img

ALU 的输入包括数据和指令码。ALU 的输出是其执行运算的结果。

img

PC寄存器，存储当前指令的地址。当CPU执行一条指令后，它会自动增加PC的值，以指向下一条要执行的指令的地址。这个增加操作被称为 INC（increment，递增）。EIP

img

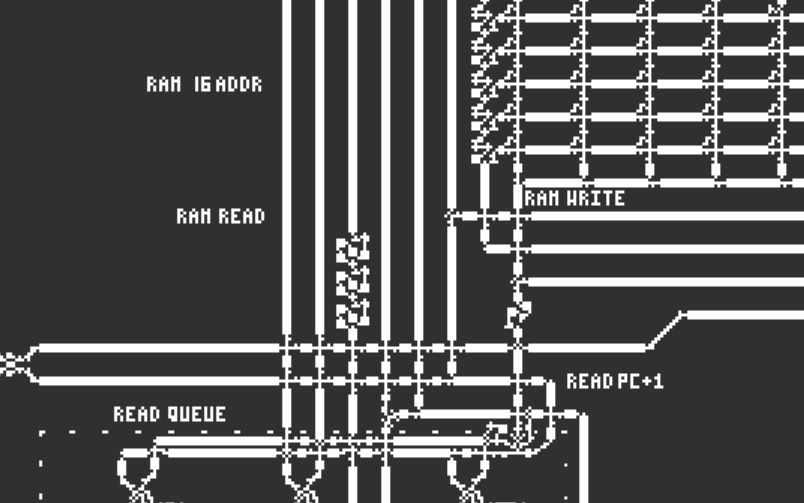
RAM（随机存取存储器）是用于存储数据和指令的存储器单元。

RAM 16 ADDR：表示RAM的地址宽度为16位，最多可以寻址65536个存储单元。

READ QUEUE读取队列——指令预取和 数据预取

img

找到一个类似的CPU——一模一样、

image-20240916153134760

image-20240916153207060

整个指令集包括11条RISC指令：

1
2
3
4
5
6
7
8
9
10
11
MNZ [test] [value] [dest] – Move if not zero; sets [dest] to [value] if [test] is not zero.
MLZ [test] [value] [dest] – Move if less than zero; sets [dest] to [value] if [test] is less than zero.
ADD [val1] [val2] [dest] – Add; adds [val1] to [val2] and stores the result in [dest].
SUB [val1] [val2] [dest] – Subtract; subtracts [val2] from [val1] and stores the result in [dest].
AND [val1] [val2] [dest] – Bitwise AND; bitwise ANDs together [val1] and [val2] and stores the result in [dest].
OR [val1] [val2] [dest] – Bitwise OR; bitwise ORs together [val1] and [val2] and stores the result in [dest].
XOR [val1] [val2] [dest] – Bitwise XOR; bitwise XORs together [val1] and [val2] and stores the result in [dest].
ANT [val1] [val2] [dest] – Bitwise AND-NOT; bitwise ANDs together [val1] and (NOT [val2]) and stores the result in [dest].
SL [val1] [val2] [dest] – Shift left; shifts [val1] left by [val2] bits and stores the result in [dest].
SRL [val1] [val2] [dest] – Shift right (logical); shifts [val1] right by [val2] bits and stores the result in [dest]. Doesn't preserve sign.
SRA [val1] [val2] [dest] – Shift right (arithmetic); shifts [val1] right by [val2] bits and stores the result in [dest], while preserving sign.

指令支持4种寻址方式，在汇编语言中用特定前缀区分：

  • 立即寻址：无前缀
  • 直接寻址：前缀A
  • 间接寻址：前缀B
  • 双重间接寻址：前缀C

ok懂了，那就先把ROM的信息拿出来——

1111

这是一个1

对应这个大图——

png1

标注0和1——

annotated_png1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import cv2
import numpy as np

image = cv2.imread('png1.png')
black_template = cv2.imread('0000.png', 0) 
white_template = cv2.imread('1111.png', 0) 

h_template, w_template = black_template.shape
image_gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
img_height, img_width = image_gray.shape

matrix = np.full((img_height // h_template, img_width // w_template), '0', dtype=str)
res_black = cv2.matchTemplate(image_gray, black_template, cv2.TM_CCOEFF_NORMED)
threshold = 0.8
loc_black = np.where(res_black >= threshold)

res_white = cv2.matchTemplate(image_gray, white_template, cv2.TM_CCOEFF_NORMED)
loc_white = np.where(res_white >= threshold)

for pt in zip(*loc_black[::-1]):
    x, y = pt
    matrix[y // h_template, x // w_template] = '0' 

for pt in zip(*loc_white[::-1]):
    x, y = pt
    matrix[y // h_template, x // w_template] = '1'  

with open('matrix_output.txt', 'w') as f:
    for row in matrix:
        f.write(''.join(row) + '\n')

根据延申方向和ROM结构，后四位是opcode，前18位为addr3，19-18*2为addr2，18*2+1到18*3为addr1，18*3+4 = 57行，

所以从右往左一列一列、从下往上、4.18.18.18读取

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
000000000000000000000000000000000000000000000000000000000
000000000001010110000000000001011000011111111111111110001
000000000000000100000000000000000000000000000000000000110
000000000000000100001100101011100110011111111111111110001
000000000000000110000111000110110100011111111111111110001
000000000000001000001010111101011010011111111111111110001
000000000000001010001100011010000110011111111111111110001
000000000000001100000001110100111110011111111111111110001
000000000000001110000110100010011110011111111111111110001
000000000000010000000101111000110110011111111111111110001
000000000000010010000001001111110100011111111111111110001
000000000000010100000111101110011110011111111111111110001
000000000000010110000010111001000010011111111111111110001
000000000000011000001000110010110010011111111111111110001
000000000000011010000111001111001110011111111111111110001
000000000000011100000010010100101010011111111111111110001
000000000000011110000011110010010100011111111111111110001
000000000000100000001010111110100000011111111111111110001
000000000000100010000100000101100110011111111111111110001
000000000000100100000110000100000100011111111111111110001
000000000000100110001011000110100100011111111111111110001
000000000000101000001000000011100110011111111111111110001
000000000000101010000011011110111000011111111111111110001
000000000000101100001011001000010010011111111111111110001
000000000000101110001010111001000110011111111111111110001
000000000000110000000110000110001010011111111111111110001
000000000000110010000011111000000000011111111111111110001
000000000000110100001101000000001100011111111111111110001
000000000000110110000111100011110110011111111111111110001
000000000000111000000011001010001110011111111111111110001
000000000000111010000000111000011100011111111111111110001
000000000000111100001011000101100010011111111111111110001
000000000000111110001100001101110110011111111111111110001
000000000001000000001000000001110100011111111111111110001
000000000001000010000010100000110010011111111111111110001
000000000001000100000111100111010010011111111111111110001
000000000001000110001011101001110110011111111111111110001
000000000001001000001011100101110100011111111111111110001
000000000001001010000110111000001100011111111111111110001
000000000001001100001011010010100110011111111111111110001
000000000001001110000000000000000000011111111111111110001
000000000001001110010010101110101010100000000000000010110
000000000000000100100000000000000100100000000001001110011
000000000001001110011001001001111100100000000000000010110
000000000000000110100000000000000110100000000001001110011
000000000001001110010100111111010110100000000000000010110
000000000000001000100000000000001000100000000001001110011
000000000001001110010010011101010010100000000000000010110
000000000000001010100000000000001010100000000001001110011
000000000001001110011111111000111110100000000000000010110
000000000000001100100000000000001100100000000001001110011
000000000001001110011000100101010100100000000000000010110
000000000000001110100000000000001110100000000001001110011
000000000001001110011011111011011010100000000000000010110
000000000000010000100000000000010000100000000001001110011
000000000001001110011111010011110010100000000000000010110
000000000000010010100000000000010010100000000001001110011
000000000001001110011001110001000000100000000000000010110
000000000000010100100000000000010100100000000001001110011
000000000001001110011100111100111010100000000000000010110
000000000000010110100000000000010110100000000001001110011
000000000001001110010110110110110110100000000000000010110
000000000000011000100000000000011000100000000001001110011
000000000001001110011001010010100010100000000000000010110
000000000000011010100000000000011010100000000001001110011
000000000001001110011100011000101100100000000000000010110
000000000000011100100000000000011100100000000001001110011
000000000001001110011101110101001000100000000000000010110
000000000000011110100000000000011110100000000001001110011
000000000001001110010101000001000010100000000000000010110
000000000000100000100000000000100000100000000001001110011
000000000001001110011010001000011110100000000000000010110
000000000000100010100000000000100010100000000001001110011
000000000001001110011000000111101100100000000000000010110
000000000000100100100000000000100100100000000001001110011
000000000001001110010101001001001100100000000000000010110
000000000000100110100000000000100110100000000001001110011
000000000001001110010110000110001010100000000000000010110
000000000000101000100000000000101000100000000001001110011
000000000001001110011101100010000100100000000000000010110
000000000000101010100000000000101010100000000001001110011
000000000001001110010101001011011110100000000000000010110
000000000000101100100000000000101100100000000001001110011
000000000001001110010100111100011110100000000000000010110
000000000000101110100000000000101110100000000001001110011
000000000001001110011000001001000000100000000000000010110
000000000000110000100000000000110000100000000001001110011
000000000001001110011101111011100100100000000000000010110
000000000000110010100000000000110010100000000001001110011
000000000001001110010011000011100100100000000000000010110
000000000000110100100000000000110100100000000001001110011
000000000001001110011001100111111010100000000000000010110
000000000000110110100000000000110110100000000001001110011
000000000001001110011101001101000100100000000000000010110
000000000000111000100000000000111000100000000001001110011
000000000001001110011110111011110100100000000000000010110
000000000000111010100000000000111010100000000001001110011
000000000001001110010101001001111010100000000000000010110
000000000000111100100000000000111100100000000001001110011
000000000001001110010010010001111010100000000000000010110
000000000000111110100000000000111110100000000001001110011
000000000001001110010110000101110000100000000000000010110
000000000001000000100000000001000000100000000001001110011
000000000001001110011100100100111000100000000000000010110
000000000001000010100000000001000010100000000001001110011
000000000001001110011001101010111110100000000000000010110
000000000001000100100000000001000100100000000001001110011
000000000001001110010101101101111010100000000000000010110
000000000001000110100000000001000110100000000001001110011
000000000001001110010101101001001100100000000000000010110
000000000001001000100000000001001000100000000001001110011
000000000001001110011000111011000110100000000000000010110
000000000001001010100000000001001010100000000001001110011
000000000001001110010101010110001110100000000000000010110
000000000001001100100000000001001100100000000001001110011
000000000000000000011111111111111100011111111111111110001
000000000000000000000000000000000000000000000000000000001
000000000000000000000000000000000000000000000000000000000

根据

屏幕截图 2024-09-15 005952

和上面的规则，hex2asm.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
from bitstring import BitArray

opcodes = {'0000': 'MNZ',
           '0001': 'MLZ',
           '0010': 'ADD',
           '0011': 'SUB',
           '0100': 'AND',
           '0101': 'OR',
           '0110': 'XOR',
           '0111': 'ANT',
           '1000': 'SL',
           '1001': 'SRL',
           '1010': 'SRA'}

modes = {'00': '',
         '01': 'A',
         '10': 'B',
         '11': 'C'}

def parse(code):
    out = ""
    count = 0 
    for l in code[::1]:
        opcode = opcodes[l[-4:]]
        arg1 = l[18*2-1:-4]
        arg2 = l[17:18*2-1]
        arg3 = l[:17]
        mode1 = modes[arg1[:2]]
        arg1 = str(BitArray(bin=arg1[2:]).int)
        mode2 = modes[arg2[:2]]
        arg2 = str(BitArray(bin=arg2[2:]).uint) //这里转无符号数
        mode3 = modes[arg3[:2]]
        arg3 = str(BitArray(bin=arg3[2:]).uint)
        out += str(count) + '. ' + opcode + ' ' + mode1 + arg1 + ' ' + mode2 + arg2 + ' ' + mode3 + arg3 +'\n'
        count+=1
    return out

code = []
asm = parse(code)
print(asm)

这里，value值不考虑负数，所以以无符号数转化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
0. MNZ 0 0 0
1. MLZ -1 44 43
2. XOR 0 0 2
3. MLZ -1 25971 2
4. MLZ -1 14554 3
5. MLZ -1 22445 4
6. MLZ -1 25411 5
7. MLZ -1 3743 6
8. MLZ -1 13391 7
9. MLZ -1 12059 8
10. MLZ -1 2554 9
11. MLZ -1 15823 10
12. MLZ -1 5921 11
13. MLZ -1 18009 12
14. MLZ -1 14823 13
15. MLZ -1 4757 14
16. MLZ -1 7754 15
17. MLZ -1 22480 16
18. MLZ -1 8371 17
19. MLZ -1 12418 18
20. MLZ -1 22738 19
21. MLZ -1 16499 20
22. MLZ -1 7132 21
23. MLZ -1 22793 22
24. MLZ -1 22307 23
25. MLZ -1 12485 24
26. MLZ -1 7936 25
27. MLZ -1 26630 26
28. MLZ -1 15483 27
29. MLZ -1 6471 28
30. MLZ -1 1806 29
31. MLZ -1 22705 30
32. MLZ -1 25019 31
33. MLZ -1 16442 32
34. MLZ -1 5145 33
35. MLZ -1 15593 34
36. MLZ -1 23867 35
37. MLZ -1 23738 36
38. MLZ -1 14086 37
39. MLZ -1 23123 38
40. MLZ -1 0 39
41. XOR A1 38357 39
42. SUB A39 A2 2
43. XOR A1 51518 39
44. SUB A39 A3 3
45. XOR A1 42987 39
46. SUB A39 A4 4
47. XOR A1 37801 39
48. SUB A39 A5 5
49. XOR A1 65311 39
50. SUB A39 A6 6
51. XOR A1 50346 39
52. SUB A39 A7 7
53. XOR A1 57197 39
54. SUB A39 A8 8
55. XOR A1 64121 39
56. SUB A39 A9 9
57. XOR A1 52768 39
58. SUB A39 A10 10
59. XOR A1 59293 39
60. SUB A39 A11 11
61. XOR A1 46811 39
62. SUB A39 A12 12
63. XOR A1 51793 39
64. SUB A39 A13 13
65. XOR A1 58134 39
66. SUB A39 A14 14
67. XOR A1 61092 39
68. SUB A39 A15 15
69. XOR A1 43041 39
70. SUB A39 A16 16
71. XOR A1 53519 39
72. SUB A39 A17 17
73. XOR A1 49398 39
74. SUB A39 A18 18
75. XOR A1 43302 39
76. SUB A39 A19 19
77. XOR A1 45253 39
78. SUB A39 A20 20
79. XOR A1 60482 39
80. SUB A39 A21 21
81. XOR A1 43375 39
82. SUB A39 A22 22
83. XOR A1 42895 39
84. SUB A39 A23 23
85. XOR A1 49440 39
86. SUB A39 A24 24
87. XOR A1 61298 39
88. SUB A39 A25 25
89. XOR A1 39026 39
90. SUB A39 A26 26
91. XOR A1 52477 39
92. SUB A39 A27 27
93. XOR A1 59810 39
94. SUB A39 A28 28
95. XOR A1 63354 39
96. SUB A39 A29 29
97. XOR A1 43325 39
98. SUB A39 A30 30
99. XOR A1 37437 39
100. SUB A39 A31 31
101. XOR A1 45240 39
102. SUB A39 A32 32
103. XOR A1 58524 39
104. SUB A39 A33 33
105. XOR A1 52575 39
106. SUB A39 A34 34
107. XOR A1 44477 39
108. SUB A39 A35 35
109. XOR A1 44326 39
110. SUB A39 A36 36
111. XOR A1 51043 39
112. SUB A39 A37 37
113. XOR A1 43719 39
114. SUB A39 A38 38
115. MLZ -1 65534 0
116. MLZ 0 0 0
117. MNZ 0 0 0

代码逻辑还是很明显的——

初始化，放一堆数字在2到38，A1依次和另一堆数字异或后减去Ai位置数放在i位

A1与38357异或后放在39位，[A39]减[A2]放在A2，[2]从25971变成12386

（异或具有对称性，得A1为-65536)

QFTASM Interpreter——https://darthnithin.github.io/qftasm-interpreter/qftasm.html

跑一下，什么都没有——怎么绘世呢？

我们可以看到，A1使用的最多，但是没有初始值——要爆破了（已知头是OOO，O是79）

知道第一位是

1
2
3
4
5
6
7
i = 0
for i in range (65536):
    value = (i^38357)
    if (value)-25971 == 79:
        break
print(i)
# 61463

把上面汇编塞一行——3. MLZ -1 61463 1，再放编译器跑一下，非常美丽的ascii出现了——

1
2
3
4
5
flag = [79,79,79,123,105,110,95,116,104,105,115,95,108,105,102,101,95,95,95,121,111,117,114,101,95,111,110,95,121,111,117,114,95,111,119,110,125]
for i in range(len(flag)):
    print(chr(flag[i]),end= '')

#OOO{in_this_life___youre_on_your_own}
文章作者: W3nL0u
文章链接: https://github.com/xyy9233/xyy9233.github.io.git/2024/09/15/defconquals-rev-nchevjuw/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 W3nL0u !
Reverse Golly DEFCON
  目录